Despedida

 Tras longos meses de redacción e entradas, chega o fin dun curso,  ultimo da nosa etapa no colexio.

 Queria agradecer a todos aqueles que estiveron ahi dende que cheguei, profesores e alumnos, os cales sempre me apoiaron en todo canto puideron. Moitas grazas por todos istes anos ensinando e aprendendo tanto.

Esperemos que o futuro depare un bo camiño a todos, e todos academos a meta que queiramos, sería toda unha ilusión ver que, dentro duns anos, todos conviven e son felices coas suas vidas.

Grazas por todo, en serio.

Unha aperta moi grande.

Toño.

Riot Games

  Riot  Games foi fundada en 2006 por  Brandon  Beck e Marc  Merrill coa intención de cambiar a forma en que se crean videoxogos para os xogadores. En 2009, lanzamos o noso primeiro xogo recoñecido mundialmente,  League  of  Legends. O xogo converteuse no xogo para  PC máis xogado no mundo e un factor crave do crecemento explosivo dos  esports. Os xogadores son a base da nosa comunidade e grazas a eles continuamos evolucionando e mellorando a experiencia de  League  of  Legends. A sede de  Riot  Games atópase en Los Ángeles,  California, e conta con 23 oficinas máis por todo o mundo.

Os nosos valores son o noso compás; guíannos ata quen queremos ser. Cara a eles miramos en busca de axuda cando non alcanzamos os nosos obxectivos, e a través deles avaliamos cada decisión que tomamos.

En 2012 redactamos un manifesto: unha declaración sobre quen criamos que eramos, unha nova empresa ao comezo da súa andaina. Fóronnos de gran axuda durante moitos anos, pero non evolucionaron connosco. Agora, necesitamos valores que representen quen queremos ser no

próximo capítulo.

A continuación, atoparedes os nosos valores actualizados. Falamos con máis de 1700 empregados de  Riot e preguntámoslles como debemos ser para cumprir o noso compromiso cos xogadores.  Co obxectivo de facer destes valores unha realidade, prometemos institucionalizalos en  Riot e facer que formen parte do día a día de todos os empregados:

Seguiremos investindo constantemente en fomentar unha contorna onde cada empregado poida crecer e alcanzar o seu máximo potencial.

Esforzarémonos para que os procesos sexan xustos e equitativos, e para que os empregados poidan confiar neles.

Os nosos líderes cumprirán cos valores e promoveranos de forma activa entre os seus equipos.

Queremos que  Riot sexa o mellor lugar de traballo para os máis apaixonados e comprometidos coa nosa misión.

Fonte: https://www.riotgames.com/es/quienes-somos/valores

Taoismo

 O  taoísmo ou  daoísmo  é unha tradición filosófica de orixe chinesa a cal salienta vivir en harmonía co  tao . A palabra chinesa 道  tao , adóitase traducir por 'vía' ou 'camiño', aínda que ten innumerables matices na filosofía e as relixións populares chinesas.

O  tao é unha idea fundamental na maioría das escolas que forman parte da filosofía chinesa; con todo, para o  taoísmo é referido como o principio de unidade absoluta, e ao mesmo tempo  mutable, que conforma a realidade suprema e o principio  cosmogónico e  ontológico de todas as cousas.​ Así, para os  taoístas o  tao constitúe a fonte, o patrón e a substancia de todo o existente.

O  Dào Dea  Jī ng  tamén coñecido como  Tao Che King ou  Tao Che  Ching, é o libro que condensa os ensinos atribuídos ao filósofo  Lao- Tse​  ou  Laocio.​ ​ E aínda que a existencia histórica de tal personalidade aínda se debate, o libro é considerado como clave para a tradición  taoísta. Xunto co  Zhuangzi considéranse os textos crave da tradición.

Fonte: https://es.wikipedia.org/wiki/Tao%C3%ADsmo

El experimento

 Nas últimas clase de psicoloxía, estivemos vendo a pelicula de "El experimento". A película trata sobre un experimento no que se dan dus roles por dúas semanas: uns seran gardas dunha prisión, e os outros serán os presos. 

A película trata distintos temas como o abuso de poder, a percepción dun mismo ou a violencia exercida pola autoridade. Unha película interesante, ainda que eso si, bastante violenta.

Cosellos para unha boa lectura compresiva

 Unha lectura comprensiva é máis que ler por enriba un texto. Unha lectura compresiva consiste en ser capaz de extraer o significado dun texto e sobre este, traballar distintas cuestións relacionadas con el.

Para unha boa lectura compresiva. requírese de un ambiente relaxado, concentración, e un habito de lectura para ser capaz de entender calquera tipo de texto que se che propoña. 

Ademais, un bo lector sempre pode ir reducindo a sua lectura en núcleos de información, facilitando así unha posterior retención de ideas.

O bo comprensor é alguén que non vai ter problemas á hora de estudar temas quizais algo máis extensos, nin sera un mal ointe cara aos demais.

Distribución Binomial

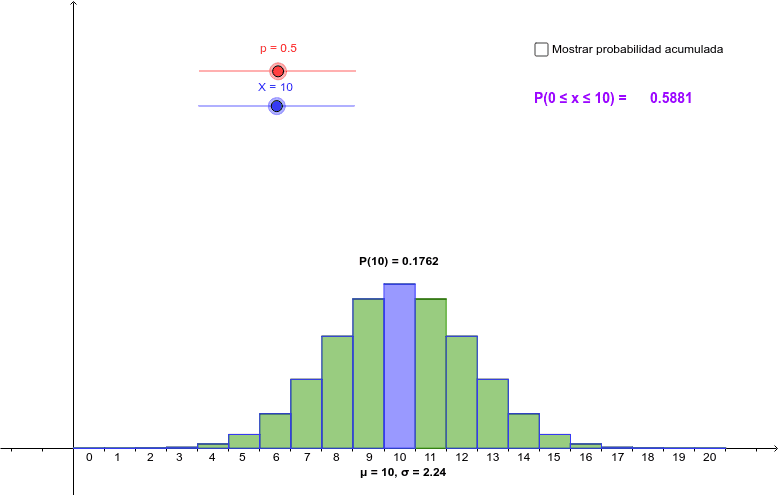
 Unha distribución  binomial, en estatística, é unha distribución de probabilidade discreta (función que asigna a cada suceso definido sobre a variable a probabilidade de que devandito suceso ocorra) que describe o número de éxitos ao realizar  n experimentos ou ensaios de  Bernoulli independentes entre si, acerca dunha variable aleatoria.

Un experimento de  Bernoulli caracterízase por ter só dous resultados. Un deles denomínase «éxito» e ao outro, «fracaso». Por exemplo, imaxínache o lanzamento dunha moeda cuxo resultado de «sacar cara» é o éxito. Se lanzamos 5 veces a moeda e contamos os éxitos que obtemos, a nosa distribución de probabilidades axustaríase a unha distribución  binomial.

Deste xeito, noutras palabras, a distribución  binomial defínese como unha serie de experimentos ou ensaios nos que só podemos ter 2 posibles resultados (éxito ou fracaso), sendo o éxito a variable aleatoria.

Por exemplo, ao lanzar un dado, a posibilidade de que o resultado sexa par ou impar será exactamente a mesma: o 50 %. E por moitas veces que o lancemos, a probabilidade, en cada unha desas veces, seguirá sendo o 50 %. Igual que no exemplo da moeda.

Na distribución  binomial hai tres variables:

n é o número de veces que repetimos o experimento.

p é un dos dous resultados ao que chamaremos éxito.

q é o outro resultado posible ao que chamaremos fracaso.

A probabilidade de cada posibilidade non pode ser máis grande que 1 e non pode ser negativa. Por iso, como  p e  q son os dous únicos resultados posibles, entre os dous a súa porcentaxe debe sumar un, polo que  p =1-  q.

Fonte: https://www.superprof.es/apuntes/escolar/matematicas/probabilidades/distribucion-binomial/

Fonética en ingles

 O inglés e outro dos idiomas nos quea pronuncia é máis complexa do que parece. Cada letra ten a súa pronuncia nun principio, é certo, pero ao mezclarese entre si, moitas delas varían a sua pronuncia, incluso dependendo da palabra, o grupo consonantico ou vocálico pronúnciase dun xeito ou doutro. Para eso, temos taboas como a seguinte, baseada na fonética, as cales debemos coñecer para facer unha correcta pronuncia ao falar no idioma anglosaxón.